추천시스템 Metric

본 게시물은 추천시스템에 대한 평가 지표에 대해 해당 포스트를 읽고 정리하는 글이다.

1. Introduction

AI/ML에 관한 project시 목표를 수행하는 모델을 설계 및 학습한 뒤 metric를 통해 모델의 성능을 평가(evaluation)해야 한다. 일반적으로 평가를 위한 metric은 task(regression, classification)에 따라 나뉘어지게 된다. 하지만 추천 시스템의 경우 아래 두가지 task를 수행해야 하기에 일반적인 평가 metric을 바로 적용하기 어렵다.

1. 아이템의 등급 예측
2. 아이템 순위가 반영된 추천 리스트 생성

따라서 이번 글에서는 추천 시스템에 대한 모델링 후 평가를 위해 아래 세 가지 순위 metric을 소개한다.

• MRR: Mean Reciprocal Rank
• MAP: Mean Average Precision
• NDCG: Normalized Discounted Cumulative Gain

2. Confusion Matrix in Recommender System

2.1 Accuracy

Accuracy (TP + TF / TP + TF + FP + FN) 에 대한 metric은 아래 두가지가 있으며 이는 실제와 예측값의 등급을 비교하는 것에 초점을 맞춘다.

• mean absolute error (MAE)
• root mean square error (RMSE)

2.2 Decision support metrics

Decision support metric은 아래 세가지가 있으며 이는 추천인이 사용자의 올바른 의사결정에 얼마나 도움이 되었는가를 측정하는 것에 초점을 맞춘다.

• Precision : 추천한 것 중 사용자가 선호하는 것의 비율 (TP / TP + FP)
• Recall : 사용자가 선호하는 것 중 추천한 것의 비율 (TP / TP + FN)
• F1 score : Precision과 Recall의 조화평균

3. Rank-less Evaluation Metrics

위 metric들은 사용자가 좋은 아이템을 선택하고 나쁜 아이템을 피하는데 도움을 줄 수 있다. 하지만 이들은 모든 데이터 셋을 대상으로 평가한 것들이기 때문에 ranking task에서는 활용하기 어렵다. 추천 시스템은 단순 아이템을 맞추는 것 보다 상위에 있는 아이템을 맞추도록 하는 것, 즉 ‘Top-N’을 타겟으로 삼아야 하기 때문이다. 예를들어 유튜브에서 수 많은 영상들을 추천 받았지만 내가 보고싶은 컨텐츠가 스크롤을 한참 내려서 봐야 한다면 추천의 성능이 좋다고 할 수 없다.

때문에 위 metric을 확장하여 Precision과 Recall에 대해 추천하는 아이템을 상위 N개로 제한하는 방법이 제안되었으며, 이를 Precision@N, Recall@N, F1@N으로 나타낸다. 하지만 이 또한 기존의 metric과 유사하며 여전히 아이템을 맞추는 것에만 집중한다는 단점이 있다.

4. Rank-Aware Evaluation Metrics

앞선 내용을 통해 추천 시스템의 목적은 관련(relevant) 아이템을 추천 리스트에서 상위에 올리는 것임을 알 수 있다. 이러한 목적을 가진 추천 시스템은 평가시 아래 두가지를 항목을 고려해야 한다.

1. 추천 시스템이 아이템을 어느 위치에 제안할 것인가?
   
2. 추천 시스템이 아이템간 상대적인 선호도를 잘 반영 하였는가?

위와같은 항목을 평가에 반영한, 추천 시스템에서 사용할 수 있는 metric을 rank-aware metric이라고 하며, 아래의 세가지가 그 예시이다.

• MRR: Mean Reciprocal Rank
• MAP: Mean Average Precision
• NDCG: Normalized Discounted Cumulative Gain

4.1 MRR

rank-aware metric의 가장 단순한 방식으로 “relevant한 항목이 첫번째로 나오는 위치”에 집중한다.

4.1.1 Algorithm

• 추천 리스트를 생성함
• 리스트에서 첫번째로 관련(relevant)있는 아이템의 위치 $k_u$를 구함
• $\frac{1}{k_u}$ 을 계산
• 모든 사용자에 대한 $k_u$ 역수의 평균
  
  

4.1.2 Example

예시의 사용자 1의 경우

STEP1. relevant한 item이 추천 리스트 중 3번째에 처음 있었기 때문에 1/3
STEP2. 사용자 2의 경우 추천 리스트 중 2번째에 처음 있었기에 1/2
STEP3. 사용자 3의 경우 추천 리스트 중 1번째에 있었기에 1로 계산할 수 있다.
STEP4. 이에대한 평균을 구하면 metric 결과는 0.61이 된다.

4.1.3 Advantages

• 계산하기 쉽고 해석하기 쉽다.
• 첫 번째 관련 요소에 높은 초점을 맞추고 있기에 “나에게 가장 적합한 항목” 인 추천 task 적합하다.
• 탐색 쿼리 또는 팩트 검색과 같은 알려진 항목 검색에 적합하다.

4.1.4 Disadvantages

• 첫번째 관심 아이템을 제외한 나머지를 평가하지 않는다.
• 아이템의 리스트를 검색하려는 사용자에게 적합한 metric이 아닐 수 있다.

4.2 MAP

이전에 살펴본 Precision@N과 같은 Top-N metric은 추천 리스트를 평가하나 순서를 간주하지 않는다는 단점이 있음을 알 수 있었다. 이는 전체 리스트를 하나의 아이템 집합으로 간주하고, 모든 추천 항목의 오차를 모두 동등하게 계산한다는 의미이다. 이를 개선하기 위한 방법 중 하나는 오류에 가중치를 부여하는 metric이다. 이는 추천 순위를 고려하여 추천 항목 중 앞쪽에 위치한 오차들에는 큰 가중치를 부여하고 하위 아이템으로 내려갈수록 오차의 중요도를 점차 낮춤으로 구현할 수 있다.

4.2.1 Algorithm

• 각 사용자에 대해 반복
• 추천 항목의 첫번째 부터 끝까지 반복
  -> relevant한 아이템이 등장하면 해당 아이템 까지를 sub-list로 취급하여 precision 계산
• precision들의 평균 계산

4.2.2 Example

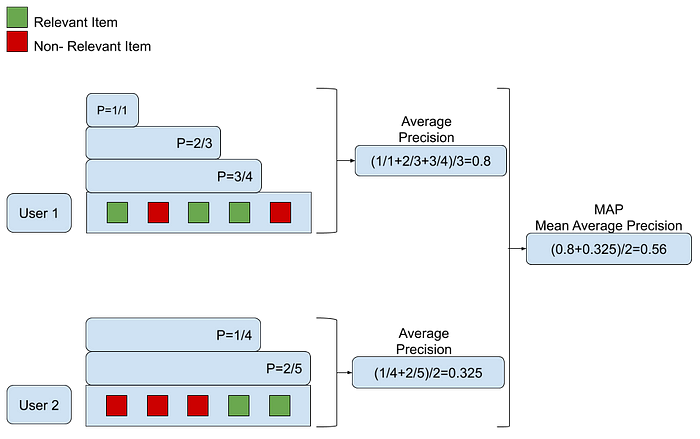
예시의 사용자 1의 경우

STEP1. 첫번째 아이템이 relevant하기에 1개의 sub-list에 대해 precision을 구함(1/1)
STEP2. 두번째 아이템은 non-relevant하기에 skip
STEP3. 세번째 아이템은 relevant하기에 3개의 sub-list에 대해 precision을 구함(2/3)
STEP4. 네번째 아이템은 relevant하기에 4개의 sub-list에 대해 precision을 구함(3/4)
STEP5. 마지막 아이템은 non-relevant하기에 skip한다.
STEP6. 위에서 구한 precision의 평균을 구한다(0.8)
STEP7. 이러한 과정을 각 사용자마다 반복하고, 평균 precision(AP)에 대한 평균(MAP)을 구한다.

각 sub-list마다 precision을 계산하는 것은 추천 리스트를 세분화 하여 평가하는 것을 의미한다.

4.2.3 Advantage

• 각 추천 리스트에 대한 평균을 구할 수 있다.
• 리스트 내 추천 아이템의 순위를 자연스럽게 반영한다.
• 추천 리스트의 상위에서 발생하는 오류에 더 많은 가중치를 부여하고 반대로, 하위에서 발생하는 오류에 대한 가중치를 줄인다.
• 이는 추천 리스트의 상위에 relevant한 아이템을 노출시키는 것에 부합한다.

4.2.4 Disadvantage

• MAP는 relevant/ non-relevant에 대한 metric이기 때문에 binary한 등급의 데이터 셋에 대해 적용할 수 있다.
• 이는 세분화된 등급에 대해서는 평가가 불가능함을 의미한다.
• 만약 세분화된 등급을 가지는 데이터 셋일 경우 임계값에 따라 binary로 바꾸는 테크닉이 필요하다.
• 이럴 경우 모든 정보를 잘 반영했다고 할 수 없다.

4.3 NDCG

NDCG metric은 MAP와 같이 관련성이 높은 아이템을 추천 리스트 상위에 올리는 것을 목표로 한다. 하지만 NDCG는 추천 리스트에 대한 평가 등급에 따라 추가적으로 조정한다. NDCG는 Normalized Discounted Cumulative Gain의 약자로 이를 구하기 위한 프로세스는 아래에서 설명한다.

4.3.1 Algorithm

• CG는 추천 리스트 중 relevant한 아이템들의 사용자 등급 합이다. 이는 단순 합이므로 위에서 살펴본 rank-less metric과 동일하다.
  ex) 추천 리스트 A, B, C에 대해 사용자 선호도가 A-0점, B-3점, C-5점 이라면 CG는 8이 된다.
• DCG-standard는 항목 위치와 비례하여 감소하는 factor를 적용 함으로 앞쪽의 아이템에 가중치를 더해주게 된다. 이로인해 추천 리스트의 등급과 위치를 모두 반영할 수 있게 된다.
  ex) 위의 예시의 경우 $DCG_{score} = 0 + 3/log(2+1) + 5/log(3+1)$
• DCG-industry는 산업에서 적용하는 방법으로 컨셉은 standard와 동일하나 relevant한 아이템의 등급에 가중치를 크게 반영한다.
• 각 유저는 다양한 추천 수를 받게된다. 이때 DCG score는 기본적으로 누적 합 컨셉을 갖고 있기 때문에 많은 추천 리스트를 받는 유저가 더 큰 값을 가지게 된다. 따라서 유저간 추천 성능을 비교하기 위해 정규화가 필요하다.
• IDCG는 DCG를 정규화 하기 위한 것으로 가장 이상적인 DCG score를 계산한 값이다.
  ex)$IDCG_{score} = 5/log(1+1) + 3/log(2+1) + 0$
• nDCG는 DCG를 IDCG로 나누어 정규화 한 값으로 0~1까지의 값을 가진다.

4.3.2 Example

4.3.3 Advantage

• 등급을 가진 아이템간의 순위를 반영할 수 있다.
• MAP에 비해 아이템의 위치를 잘 평가할 수 있다.
• 다른 추천 시스템에 대해 일관되게 더 나은 평가를 할 수 있게 한다.

4.3.4 Disadvantage

• 등급에 대한 불완전한 데이터를 받은 경우 결측치를 채우는 방식에 대한 문제가 있다. 0으로 채우게 된다면 non-relevant한 것으로 간주되기 때문이다.
• IDCG가 0일 경우 정규화를 할 수 없기에 예외 케이스를 두어야 한다. 이럴경우 NDCG도 0으로 처리하는 것이 대부분이다.

5. Conclusion

추천 시스템은 평가 단계시 추천 리스트에 대한 성능 평가를 수행해야 하며 이는 추천하는 아이템의 예측 뿐만 아닌 리스트 내 아이템의 순위(=위치)를 고려해야한다. 이를 반영한 metric은 MRR, MAP, NDCG가 있으며 보유한 데이터가 relevant/non-relevant 인지, rating이 있는지에 따라 선택적으로 반영해야 한다.